Supernovaen, der i dag er kendt som Krabbetågen, blev iagttaget i Kina og Japan i 1054. Den blev måske også iagttaget andre steder, men der er kun nedskrevne beretninger fra de to lande.
Når man omregner fra den kinesiske kalender, får man den præcise dato for supernovaens tilsynekomst, 4. juli 1054.
According to the Annals of the Sung Dynasty (the Sung-shih), on the first day of the chi-ho reign period, during the 5th month, on the chi-chou, a “guest star” appeared to the south east of Tian-kuan. The guest star was so bright that it could be seen during the daytime, and it remained so for 23 days. After that, it gradually dimmed, finally fading from visibility after two years. Japanese records also mention the star.
Fra Supernova Educator Guide, https://xmm.sonoma.edu/edu/supernova/snguide5.pdf
Billedet til højre er det mest detaljerede, der indtil nu er lavet. Se originaludgaven på websiden https://esahubble.org/images/heic0515a/. Der er også billeder i højere opløsning.
Credit:
NASA, ESA and Allison Loll/Jeff Hester (Arizona State University). Acknowledgement: Davide De Martin (ESA/Hubble).
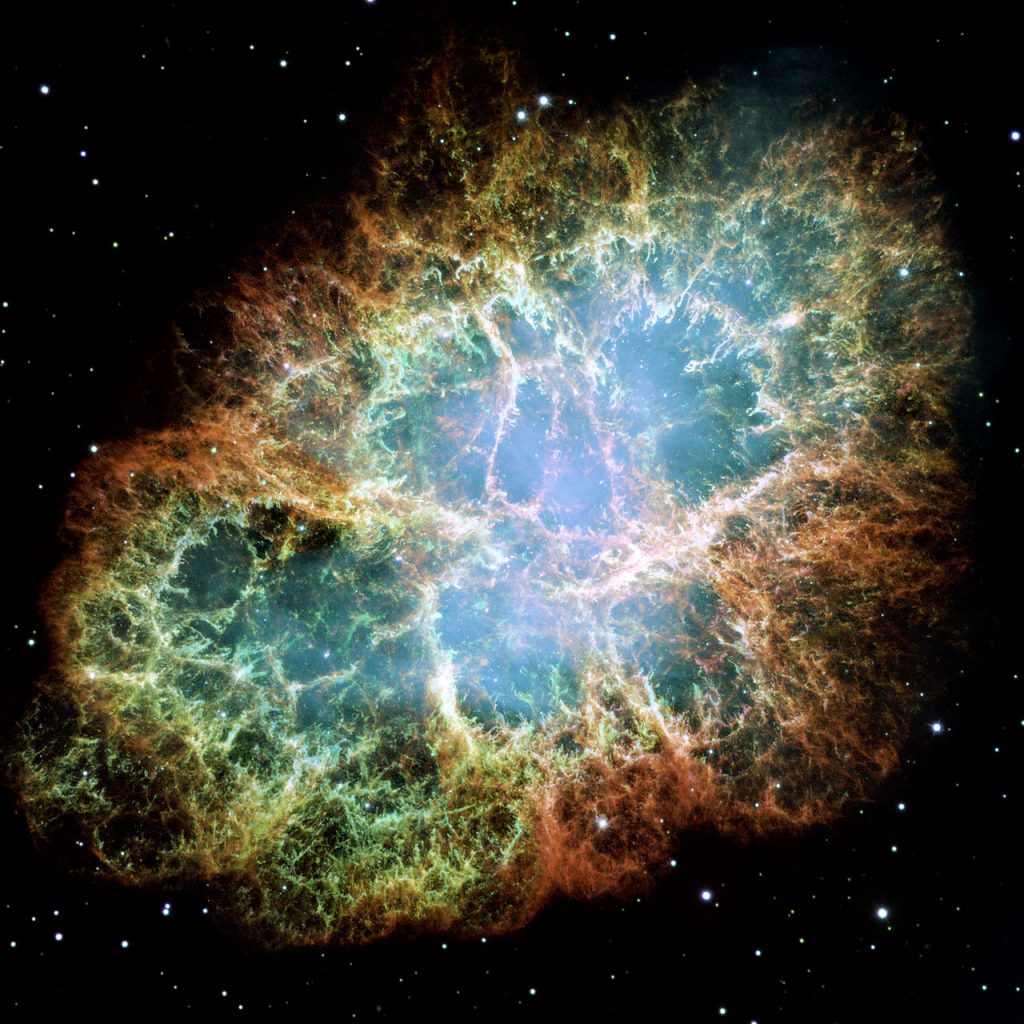
I “Supernova Educator Guide” er der forslag til en aktivitet, hvor man ud fra to billeder af krabbetågen regner tilbage og derved finder tidspunktet for dannelsen af krabbetågen. Den amerikanske version er særdeles grundig. Her følger en lidt kortere udgave af aktiviteten, der i den amerikanske udgave hedder “Crawl of the Crab”.
Vi går ud fra de følgende to billeder af krabbetågen:
Man har – i tidsrummet mellem de to billeder blev optaget – opdaget at supernova-eksplosionen har ”efterladt” en neutronstjerne i Krabbetågens centrum. Neutronstjernen er en pulsar, dvs. et objekt, der udsender elektromagnetisk stråling med bestemte tidsintervaller. Man kender pulsarens præcise placering, og vi kan derfor se på, hvor langt væk de forskellige dele af Krabbetågen er kommet fra 1956 til 1999. Ti steder er afmærket på de to billeder.
Man kan selvfølgelig måle afstande fra pulsaren til hvert af de ti afmærkede steder med lineal, men man kan også bruge et grafikprogram. Jeg bruger Irfanview.
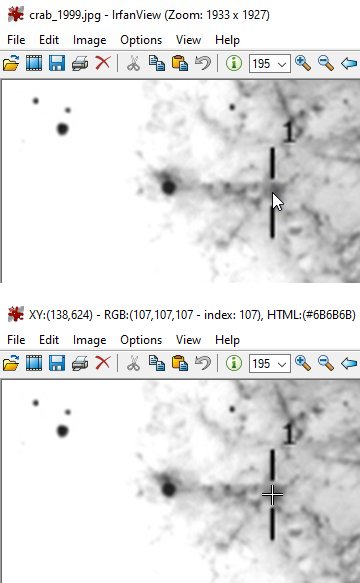
Når billedet er indlæst, kan man flytte markør-pilen til hvert af de afmærkede steder, og når man klikke på stedet ændres markør-pilen til et ┼, og punktets koordinater kan aflæses. I eksemplet til højre som (138,624).
Det skal man gøre for pulsaren og de 10 afmærkede steder.
Den videre databehandling foregår i et regneark, hvor man kan indtaste de aflæste koordinatsæt. Find regnearket her: Crawl of the Crab Excel file (højreklik og gem).
Når alle data er indtastet, beregner regnearket resten:
- De ti objekters afstande til pulsaren i 1956 og 1999.
- Afstandsændringen for hvert objekt fra 1956 til 1999.
- Den hastighed, objekterne har bevæget sig med fra 1956 til 1999 beregnes. Hastighed = afstandsændring divideret med tiden.
- Antag, at objekterne i krabbetågen har bevæget sig med samme hastighed hele tiden. Da supernovaen blev dannet, var alle objekter samme sted, nemlig der, hvor pulsaren er nu. Da vi kender afstanden fra objekt til pulsar i 1999, kan vi finde tiden som 1999-afstanden mellem pulsar og objekt, divideret med objektets hastighed.
Jeg har aldrig brudt mig om “Black box”-beregninger, så jeg har bedt eleverne om
- at undersøge formlerne i regnearkets celler, med henblik på at forstå de beregninger, der bliver udført undervejs
- at gennemføre beregningerne for ét af objekterne med lommeregner, og sammenholde regnearkets beregninger med lommeregner-resultaterne.
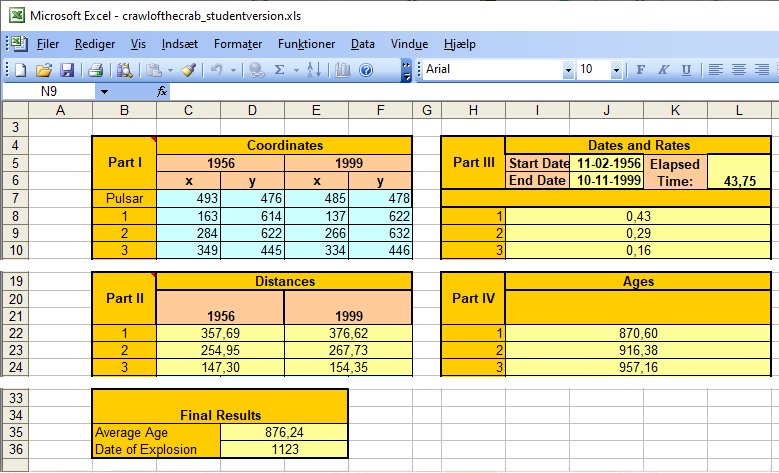
Til højre ses et udsnit af regnearket med mine aflæsninger af koordinatsættene for objekterne 1-3, og de deraf følgende beregninger. Slutresultatet er baseret på alle ti objekter, og giver en gennemsnitsalder på 876 år, svarende til at supernova-eksplosionen er sket i 1123.
Aktiviteten “Supernova Educator Guide” kan findes to steder
https://imagine.gsfc.nasa.gov/educators/programs/fermi/classroom/supernova.html
https://xmm.sonoma.edu/edu/supernova/ (Den oprindelige side, opdateres ikke)
Sidst redigeret 2022-03-15

